基于 LoserTree 的 Paimon 多路归并优化

Posted on by hackdl
摘要：
在多路归并的排序中，比较次数对整体排序的耗时影响很大。本文主要介绍在 Paimon SortMergeReader 的多路归并实现中，利用 LoserTree 替换堆排序算法，减少多路归并比较次数的设计思路以及取得的性能收益。主要包含以下几个方面：
  1. 背景介绍：介绍 Paimon 中读取数据的原理及优化思路；
  2. 多路归并算法：介绍堆排序和 LoserTree 的实现原理，并对算法复杂度进行分析和对比；
  3. 方案设计：分析在 Paimon 中使用 LoserTree 存在的问题，并提出一个基于 LoserTree 的优化实现；
  4. 算法证明：对新的实现算法进行了正确性分析和证明；
  5. 性能收益
    ：介绍在整体实现落地后
    通过基准测试
    取得的性能收益。

一、背景

在 Paimon 的 SortMergeReader 中，会对多个 RecordReader 返回的 Key-Value 进行读取，并将相同的 Key 使用 MergeFunction 进行合并，其中每个 RecordReader 的数据是有序的。整个读取过程实际上是对多个 RecordReader 的数据进行多路归并。在归并过程中，数据之间的比较次数越多，整体排序耗时越高。
多路归并的算法主要有堆排序、胜者树和败者树等。在这三种算法中，堆排序每次进行堆调整都需要和左右子节点进行比较，比较次数为 2logN，而胜者树和败者树调整时的比较次数都是 logN，区别是胜者树需要和兄弟节点进行比较并更新父节点，而败者树只需要和父节点进行比较，访存次数更少。目前在 Paimon 中默认使用堆排序实现 SortMergeReader，因此考虑使用 LoserTree 减少比较次数，在进行大量数据的读取时减少比较次数，从而提高性能。

二、多路归并算法介绍

多路归并算法主要用于外排序，主要按照排序-归并的策略进行。当需要处理的数据量非常大，内存无法全量装入时，会将这些数据先组织为多个有序的子文件，然后再对这些子文件进行归并。在 Paimon 中，每个 RecordReader 已经是有序的，因此我们只需要进行归并流程
操作
。下面会主要对堆排序和 LoserTree 算法进行介绍，并对两者间的性能进行分析对比。

2.1 堆排序

堆排序是以堆作为排序的数据结构设计的算法。堆是一棵完全
二叉树
，根据父节点中存储的值是否都大于或小于子节点的值，又分为大根堆和小根堆。以小根堆为例，排序过程分为建堆和堆调整两个过程。在整个排序过程中，如果父子节点进行比较后发生了数据交换，那么会产生自顶向下的调整，这种调整每次都需要和两个子节点同时进行比较。
1.建堆
假设有

5

个待排序列，第一步需要将这

5

个待排序列的按照头元素的大小调整为小根堆，调整的顺序为自底向上。
1）
首先调整 Node4

节点；
2）
然后调整 Node3

节点；
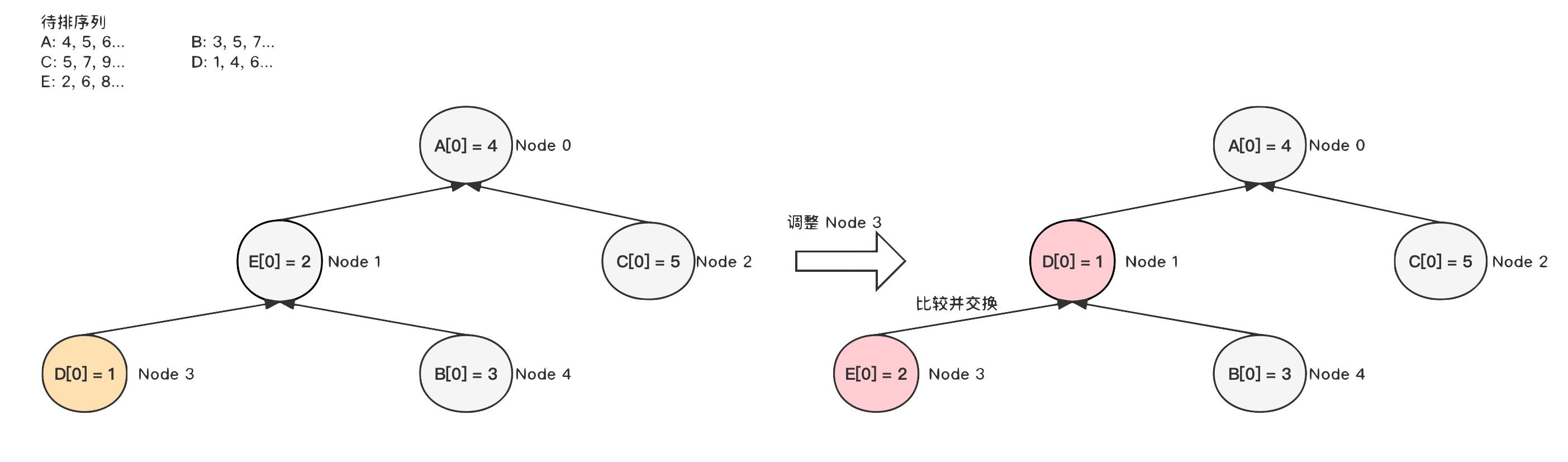
3）
调整 Node2

节点时，由于比父节点 Node0 大，因此不需要调整；
4）
继续调整 Node1

节点，由于 Node1

比 Node0

节点小，首先需要和 Node0

交换，然后再继续向下调整。至此，小根堆构建完成。
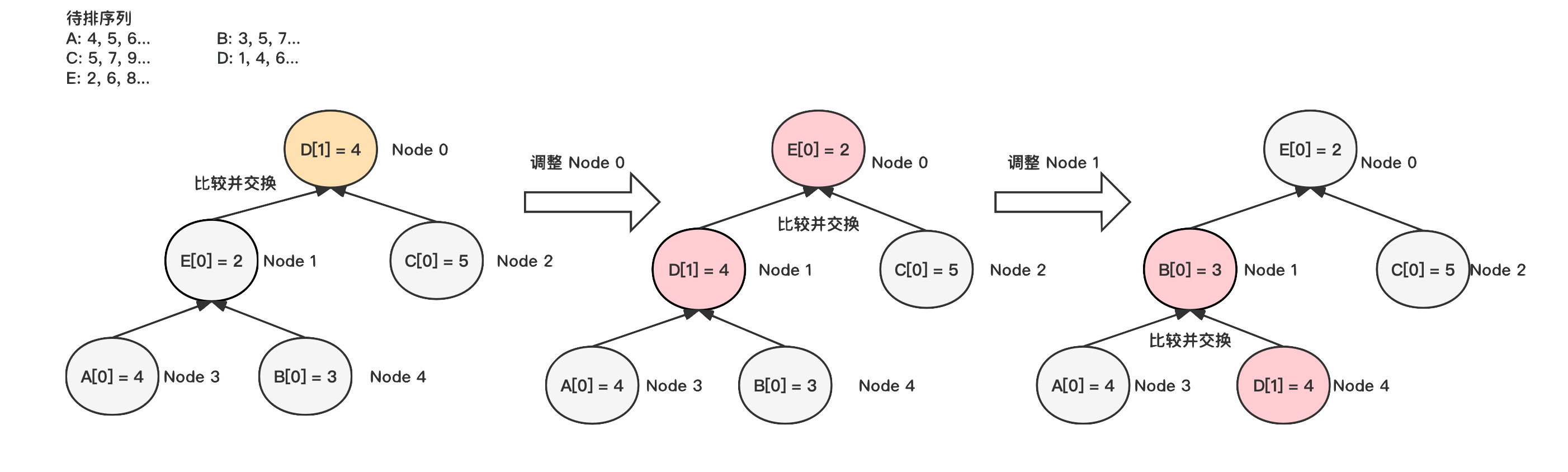
2.堆调整
每次排序时会从头节点取出当前最小的数据，将对应序列的下一个元素放到头结点，然后再自顶向下不断进行调整。每次向下调整时需要和左右两个子节点同时进行比较，选出最小值。
3.复杂度分析
假设待排序列数为 N，待排元素总个数为 n，则：
1）
空间复杂度为 O(N)
；
2）
整体排序完成的时间复杂度为 O(nlogN)
；
3）
单次调整的时间复杂度为 O(logN)，由于需要和两个子节点都进行比较，因此单次调整的比较次数为

2logN
。

2.2 LoserTree

LoserTree 也是一种常用于归并排序算法中的数据结构
，
它也是一棵完全
二叉树
。在这棵完全二叉树中，叶子节点代表待排序列，非叶子节点代表两个子节点中的败者。对于 Node0，代表全局
W
inner。相比堆排序，LoserTree 可以简化树的调整过程，由于中间节点中记录的是上次比较的败者，这个败者也等价于该节点到对应叶子节点子树的局部胜者，这样每次重新调整时只需要自底向上不断和父节点比较即可获得新的全局
W
inner。和堆排序类似，LoserTree 的排序过程分为树初始化和树调整两个过程。
1.树初始化
LoserTree 的初始化过程也是从底向上，从后往前进行，失败者成为中间节点，胜者继续向上进行比较。
1）
调整叶子节点 Leaf4，由于父节点当前还没有败者，因此设置为 Leaf4；
2）
调整叶子节点 Leaf3，和父节点中记录的败者 Leaf4

进行比较，Leaf3

获胜，继续向上。由于节点 Node2

暂时没有败者，因此设置为 Leaf3。
3）
调整叶子节点 Leaf2，和叶子节点 Leaf4

类似，将父节点的败者设置为 Leaf2；
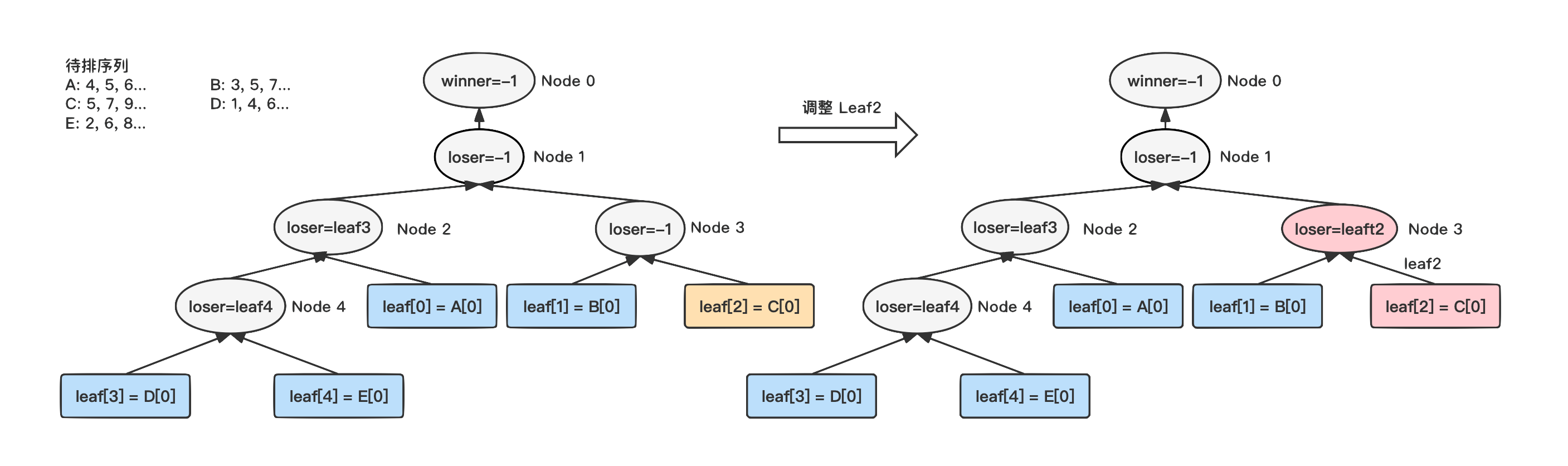
4）
继续调整叶子节点 Leaf1，和父节点中记录的败者 Leaf2

进行比较，Leaf1

获胜，继续向上，将节点 Node1

的败者设置为 Leaf1。
5）
最后调整叶子节点 Leaf0，和父节点中记录的败者 Leaf3

进行比较，Leaf3

获胜，将节点的败者设置为 Leaf0。Leaf3

继续向上和 Node1

中的败者 Leaf1

比较，最终 Leaf3

获胜，更新 Node0

中的全局胜者为 Leaf3。至此，LoserTree 的初始化过程结束。
2.树调整
和堆排序类似，每次都会从头
节
点取出一个数据，区别是堆排序是自顶向下进行调整，LoserTree 是自底向上进行调整。将对应的叶子节点待排序列元素后移一个，然后自底向上不断进行比较，直到到达头结点，得出新的全局胜者。
3.复杂度分析
假设待排序列数为 N，待排元素总个数为 n，则：
1）
空间复杂度为 O(N)
；
2）
整体排序完成的时间复杂度为 O(nlogN)
；
3）
单次调整的时间复杂度为 O(logN)，每次调整只需要和父节点进行比较，单次树调整的比较次数为 logN
。

2.3 算法对比

根据前面介绍的两种算法的复杂度分析来看，两种算法的空间复杂度和时间复杂度相同，区别是比较次数的差异，在进行树调整时，LoserTree 的调整过程更加简单，理论上 LoserTree 可以比堆排序减少一半的比较次数。在元素比较的开销比较大时，通过减少比较次数带来的收益是很明显的。因此在后续的优化方案实现中，我们选择了 LoserTree 作为排序的基本数据结构。

三、LoserTree 优化方案

在常规的 LoserTree 实现中，只需要初始化 LoserTree 之后，不断从树顶取出全局
W
inner 后，再自底向上对树进行调整即可。在 Paimon 中，SortMergeReader 需要对相同的
U
serKey 完全 Merge 之后才能返回，但同一个 RecordReader 将会复用
J
ava
对象进行数据返回，并且在 MergeFunction 中也有可能会缓存之前返回的对象，因此我们在进行树调整时，不能直接将 RecordReader 迭代到下一个数据，这会影响到之前返回的对象。虽然采用深拷贝等方法可以解决该问题，但是拷贝的开销太大，甚至产生负面效果。
因此需要提供一个 LoserTree 的变种实现：在每轮相同
U
serKey 合并完成之后，再对 RecordReader 进行数据迭代。

3.1 前置条件

  1. 在 Paimon 中每个 Key 由两部分组成：
    U
    serKey +
    S
    equenceNumber；
  2. 每个 RecordReader 中的数据是有序的，且单个 RecordReader 中不包含相同的
    U
    serKey。

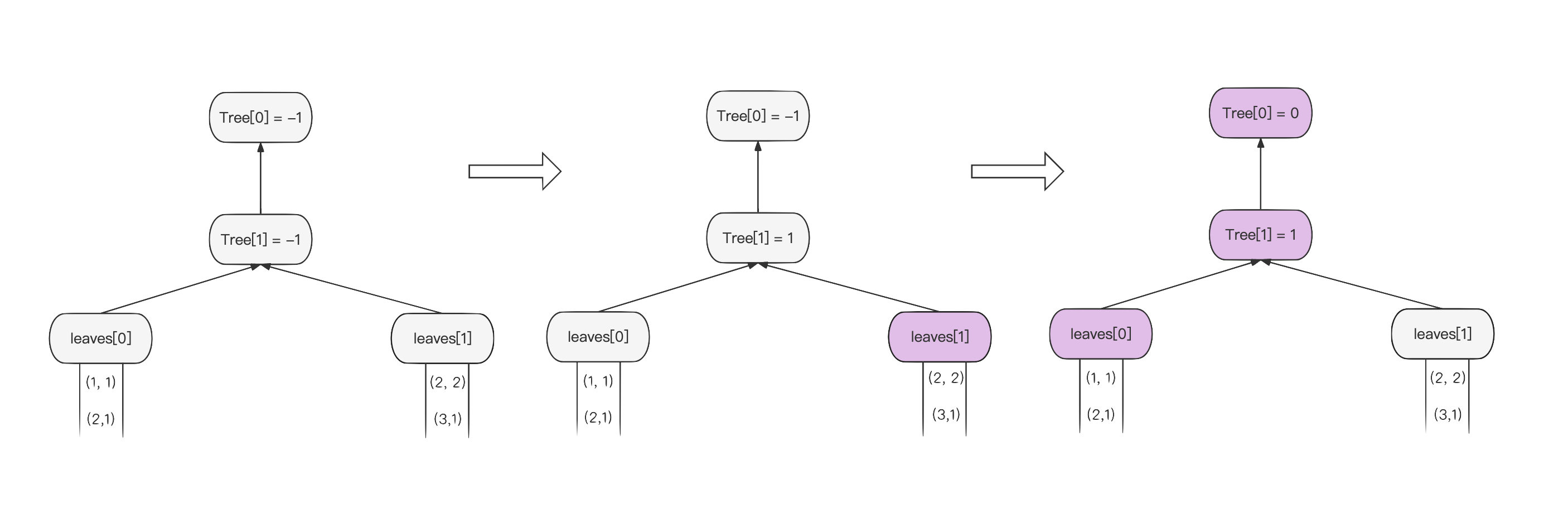
3.2 初始化

和常规 LoserTree 的初始化方式一致，由底向上构建 LoserTree，失败者成为中间节点，胜者继续向上比较。

3.3 排序

在进行树的调整时，由于对象复用的问题，我们不能直接将 RecordReader 迭代到下一个数据，需要先对数据进行标记，类似于将
S
equenceNumber 置为无限大，再自底向上进行调整，这样具有相同
U
serKey 的节点最终都可以被访问到。每次进行树调整时，
U
serKey 比较的开销比较大，我们在之前调整 LoserTree 的过程中，与待调整节点
U
serKey 相同的节点已经进行过比较，可以直接复用之前的比较结果，因此在节点比较时引入了
状态机
来做状态转换，避免重复比较。
  • 状态定义
一共定义了

6

种状态代表处于不同状态的节点。
  1. WINNER_WITH_NEW_KEY
    ：与上一次的全局
    W
    inner 使用不同的
    U
    serKey；
  2. WINNER_WITH_SAME_KEY
    ：与上一次的全局
    W
    inner 使用相同的
    U
    serKey，但
    S
    equenceNumber 更大；
  3. WINNER_POPPED
    ：全局
    W
    inner 已经被取出处理了，也用于判断在树中是否还有未处理的相同
    U
    serKey 节点；
  4. LOSER_WITH_NEW_KEY
    ：和最近一个战胜它的
    L
    ocal
    W
    inner 不具有相同的
    U
    serKey；
  5. LOSER_WITH_SAME_KEY
    ：和最近一个战胜它的
    L
    ocal
    W
    inner 具有相同的
    U
    serKey；
  6. LOSER_POPPED
    ：和最近一个全局
    W
    inner 具有相同的
    U
    serKey，并且已经被取出处理了；
  • 状态转换
两个节点在进行比较并进行状态转换时，按照以下规则进行：
  1. 每个叶子节点迭代产生的新 Key，状态初始化为 WINNER_WITH_NEW_KEY；
  2. 当树的头结点被取出时，对应的叶子节点状态切换为 WINNER_POPPED，可以看作
    U
    serKey 不变，但将
    S
    equenceNumber 设置为无限大；
  3. 根据
    L
    ocal
    W
    inner 的状态，在遇到不同状态的父节点时，会进行不同的状态转换：
  • L
    ocal
    W
    inner 的状态是
    WINNER_WITH_NEW_KEY
    ，父节点的状态是：
    • LOSER_WITH_NEW_KEY：
      两个节点需要进行比较并计算出新的
      W
      inner；如果两个节点的
      U
      serKey 相同，败者节点的状态转换为 LOSER_WITH_SAME_KEY；
    • LOSER_WITH_SAME_KEY：
      这是一个不可能发生的
      C
      ase，因为 WINNER_WITH_NEW_KEY 意味着开启了新的一轮调整，因此所有和上一次全局
      W
      inner 具有相同
      U
      serKey 的节点都应该被处理了
      ；
    • LOSER_POPPED：
      无需比较，父节点获胜并切换为 WINNER_POPED，子节点切换为 LOSER_WITH_NEW_KEY
      。

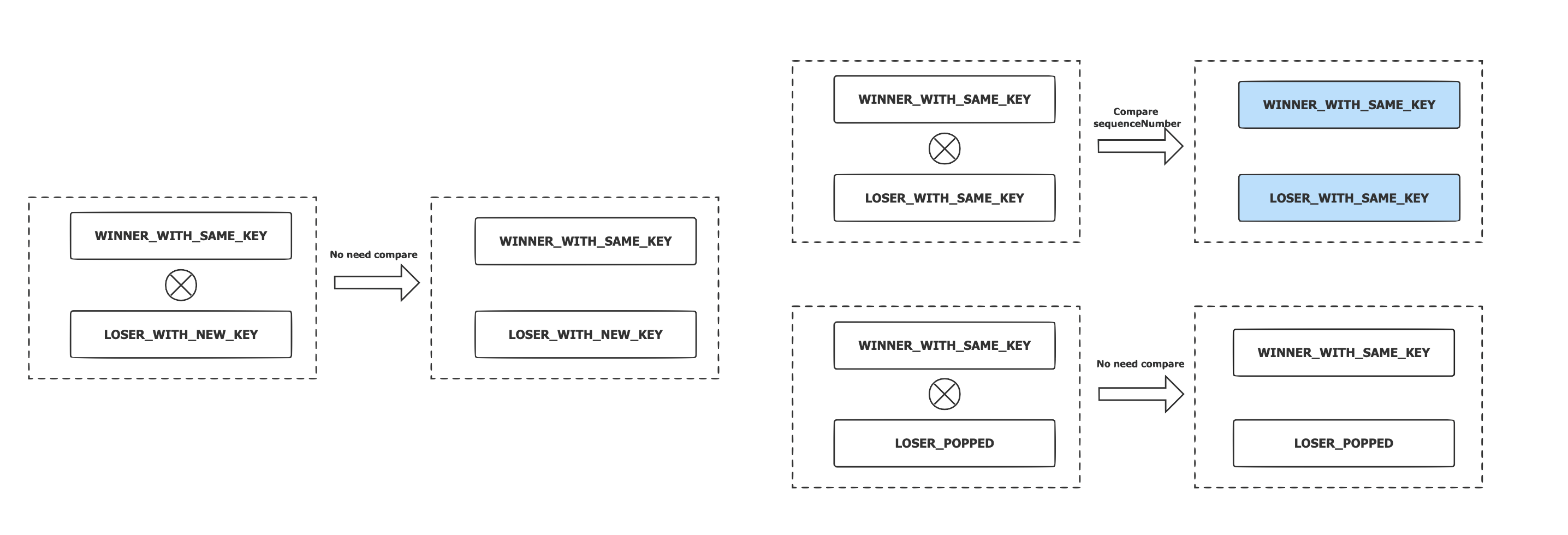
  • Local Winner 的状态是 WINNER_WITH_SAME_KEY，父节点的状态是： 

    • LOSER_WITH_NEW_KEY：无需比较和转换状态，子节点获胜； 
    • LOSER_WITH_SAME_KEY：两个节点的 UserKey 相同，只需要比较两个节点的 SequenceNumber，可以减少比较的开销。胜者切换为 WINNER_WITH_SAME_KEY，败者切换为 LOSER_WITH_SAME_KEY；
    • LOSER_POPPED：无需比较和转换状态，子节点获胜。
  • L
    ocal
    W
    inner 的状态是
    WINNER_POPPED
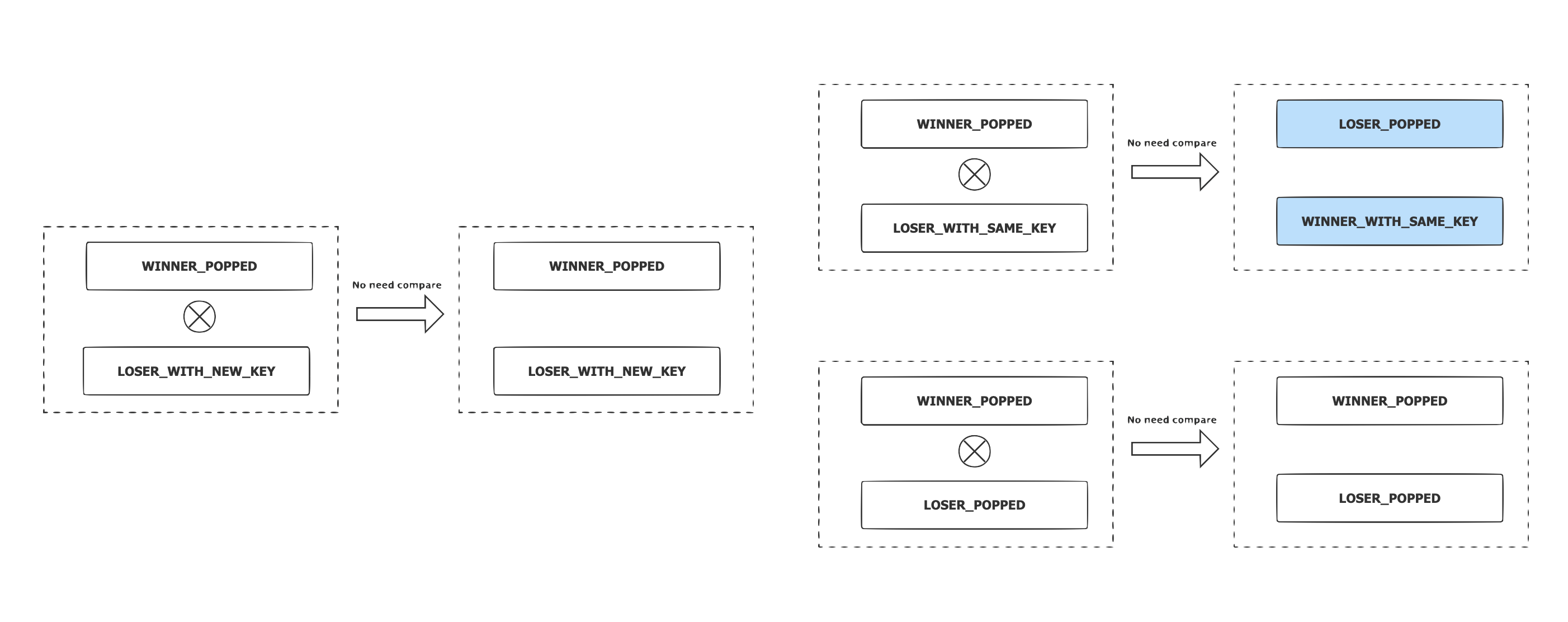
    ，父节点的状态是:
    • LOSER_WITH_NEW_KEY：无需比较和转换状态，子节点获胜
      ；
    • LOSER_WITH_SAME_KEY：无需比较，父节点获胜并将状态切换为 WINNER_WITH_SAME_KEY，子节点的状态切换为 LOSER_POPPED
      ；
    • LOSER_POPPED: 无需比较和转换状态，子节点获胜。

3.4 优化

按照上述算法可以获得一个 LoserTree 的变种实现，但每次从头节点取出一个数据后，无论当前树中是否还有未取出的相同
U
serKey 节点，这个节点都需要自底向上重新进行调整一次。极端情况下，当整个树中没有重复的
U
serKey 节点时，我们每取出一个全局
W
inner 后，需要做两次树调整：1）将
S
equenceNumber 置为无限大；2）将 RecordReader 的数据向后迭代一次。这样 LoserTree 性能反而可能会比堆排序更差。
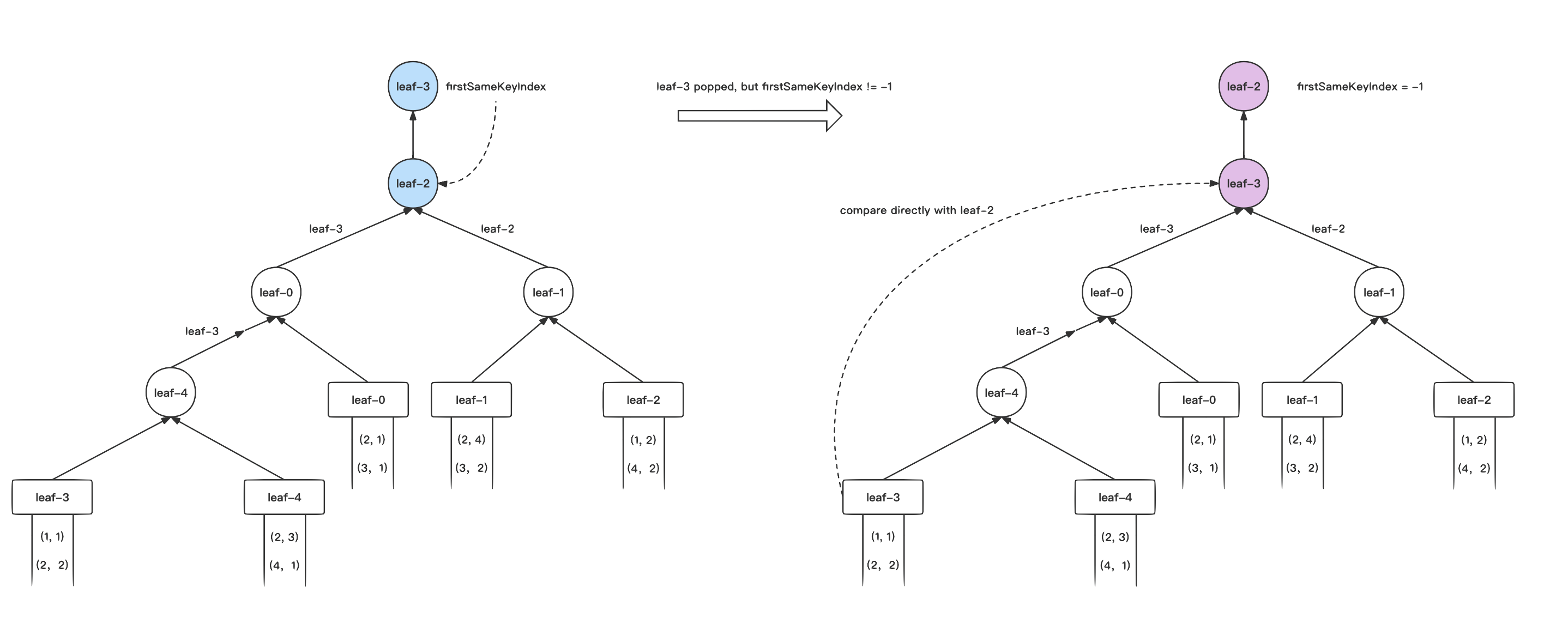
通过在叶子节点中增加
F
irstSameKeyIndex
字段，用于记录我们首次战胜的相同
U
serKey 的节点位置，这样我们可以快速区分出树中是否有相同的未处理
U
serKey 节点，如果有，我们可以直接将这两个节点的状态进行替换，并从这个位置向上进行调整，从而减少调整的层数。

四、算法证明

在 Paimon 中，LoserTree 的每一轮迭代都会合并所有相同的
U
serKey，然后再迭代相应的 RecordReader。 因此，我们只需要证明本轮同一个
U
serKey 的所有数据都会被返回即可。
Theory
：当全局
W
inner 的
F
irstSameKeyIndex 为

-1

时，树中没有与全局
W
inner 具有相同
U
serKey 的未处理节点。
Proof
：根据 LoserTree 的定义，它的任何一个子树都是 LoserTree。假设当前的全局
W
inner 来自叶子节点 A，并且在树中有一个叶子节点 B 和全局
W
inner 的 userKey 相同但还没有被处理。A 和 B 的最近共同祖先是节点 C，分别来自 C 的左右子树。
已知节点 A 必定会参与节点 C 的比较，由于节点 B 和节点 A 具有相同的最小
U
serKey，那么节点 B 要么成为右子树的
W
inner，要么被具有相同
U
serKey 的节点击败。最终节点 C 右子树的获胜者一定是与节点 A 具有相同
U
serKey 的节点，所以节点 A 的
F
irstSameKeyIndex 不能为 -1。 这证明了当全局
W
inner 的
F
irstSameKeyIndex 为

-1

时，树中不会存在与全局
W
inner 的
U
serKey 相同的未处理节点。

五、性能收益

基于 JMH 框架，我们进行了
U
serKey 分别为 Integer 和

128

位 String 类型，在不同数量的 RecordReader 和不同数据量上的读取性能基准测试，LoserTree 整体表现优于堆排序，
U
serKey 的类型越复杂，进行比较的开销越高，优化效果越明显。
  • 测试环境
    ：
    Docker
    镜像使用
    A
    pache/
    F
    link
    :1.16.1-java8，CPU 配置

    4 核，内存配置

    8G，
  • 测试结果
    ：在
    U
    serKey 为简单类型 Integer 时，优化效果大约

    10%，在
    U
    serKey 为

    128

    位 String 类型的情况下，性能可以提升

    30%

    到

    50%。
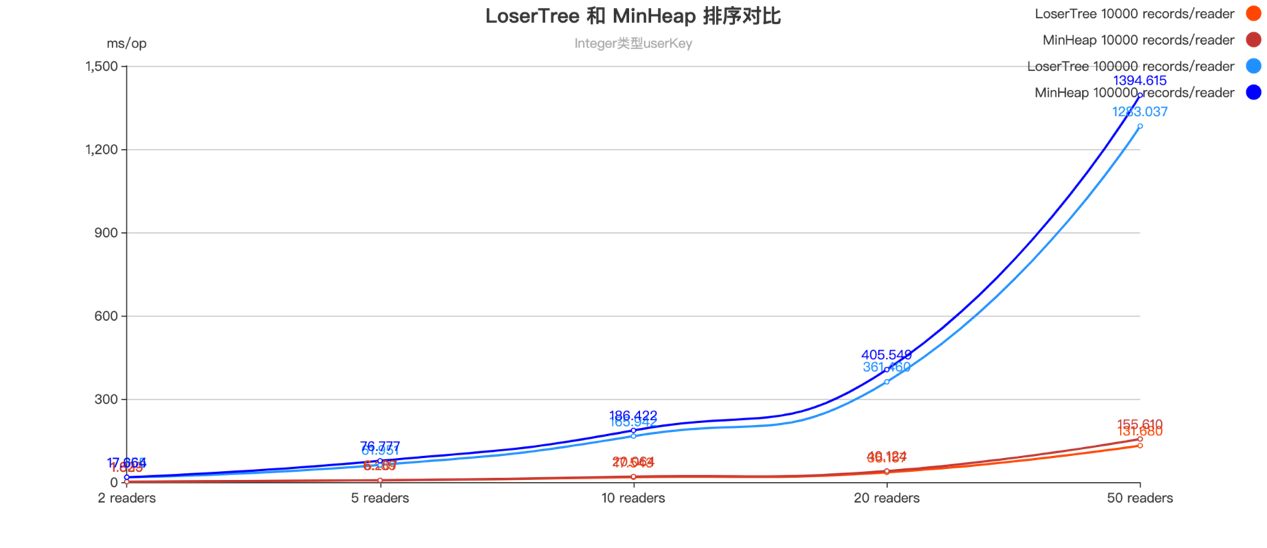
Integer 类型 userKey
128位 String 类型 userKey

*引用

  1. K-way_merge_algorithm：
    https://en.wikipedia.org/wiki/K-way_merge_algorithm#
  2. Github
    Pull Request：
    https://github.com/apache/incubator-paimon/pull/833
  3. Apache Paimon 官网：
    https://paimon.apache.org/
  4. Apache Paimon
    Github
    ：
    https://github.com/apache/incubator-paimon
  5. Apache Paimon 钉钉交流群：10880001919

*作者信息

李明，字节跳动基础架构工程师，
Apache
Flink
& Paimon Contributor
 

服务器托管，北京服务器托管，服务器租用，机房机柜带宽租用

服务器托管

咨询：董先生

电话13051898268 QQ/微信93663045！

上一篇:
下一篇: