你好呀,我是歪歪。
上周我不是发了《我试图给你分享一种自适应的负载均衡。》这篇文章嘛,里面一种叫做“自适应负载均衡”的负载均衡策略,核心思路就是从多个服务提供者中随机选择两个出来,然后继续选择两者中“负载”最小的那个节点。
前几天有读者看了文章后找到我,提出了两个问题。
有点意思,我给你盘一下。
第一个问题
第一个问题是这样的:
他的图片,指的是文章中的这个部分:

当时我也没有细看,所以我的回复是 timeout 是个配置项,我这里取出来都是 30000 的原因是因为我没有进行配置。
然后,他对于问题进行了进一步的描述:

我点到源码里面一看,好家伙,它是这样写的:
int timeout1 = getTimeout(invoker2, invocation);
int timeout2 = getTimeout(invoker2, invocation);两次调用 getTimeout 方法的入参一模一样。这个地方你用脚指头想也应该能知道它的参数传递错误了嘛。
我甚至能猜到作者写这一行代码的时候,按了一个 ctrl+d 快捷键,复制了一行出来,结果只是把前面的 timeout1 改成了 timeout2,忘记改后面了。
这种低级错误…
我也犯过好几次。

然后我叫这个读者可以去提一个 pr,以后出去吹牛的时候就可以说:我曾经给 apache 顶级开源项目贡献过源码。
但是这个读者可能比较低调,把这个机会让给我了。
于是…
我就厚着脸皮去提 pr 了,然后被 merge 了:
https://github.com/apache/dubbo/pull/12636

把 invoker2 修改为 invoker1,搞定。
舒服了,在我四处混 pr 的光荣事迹中,又添加了浓墨重彩的一笔。

第二个问题
第二个问题,其实我在之前的文中也提到了。
文章里面对于“随机选择两个”出来这个动作的代码实现,我感觉是有 BUG 的,所以提出了一个大胆的质疑:
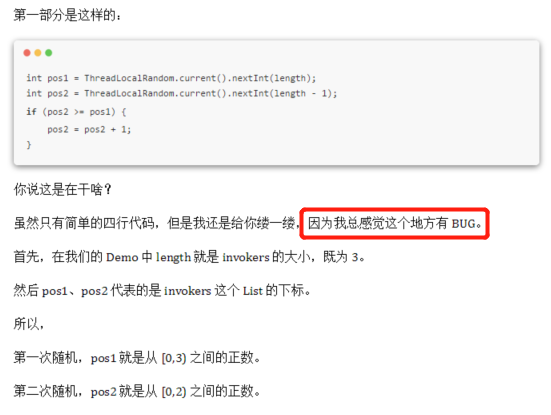
但是秉着“又不是不能用”的核心思路,当时也没有细想。
当我前面的那个 pr 被 merge 的时候,我决定:要不好人做到底,把这个 BUG 也帮它们修复一下吧。
首先,我来详细解释一下,我为什么会认为这个地方有 BUG。
首先,把它的整个源码拿过来:
int pos1 = ThreadLocalRandom.current().nextInt(length);
int pos2 = ThreadLocalRandom.current().nextInt(length - 1);
if (pos2 == pos1) {
pos2 = pos2 + 1;
}我就以最简单的情况,只有三个服务提供者,即 length=3,然后随机选两个出来,这种情况来进行说明。
我也不进行数学论证了,直接就是给你表演一个穷举大法。
首先,我们的 invokers 集合里面有三个服务提供方,invoker1,invoker2,invoker3:
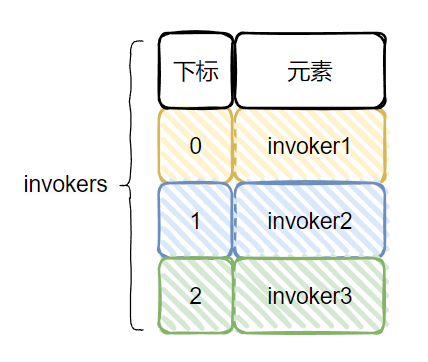
当执行这一行代码的时候:
int pos1 = ThreadLocalRandom.current().nextInt(length);
length=3,即
int pos1 = ThreadLocalRandom.current().nextInt(3);
所以 pos1 的取值范围是 [0,3)。
前面说了,我要用穷举大法,所以我们要分析 pos1 分别为 0,1,2 的时候。
pos1=0
首先,我们分析 pos1=0 的情况。
当 pos1=0 时,我们要算 pos2 的值,当执行这行代码的时候:
int pos2 = ThreadLocalRandom.current().nextInt(length – 1);
它的取值范围是 [0,2)。
所以,经过两行随机的代码之后,我们能得到这样的组合:
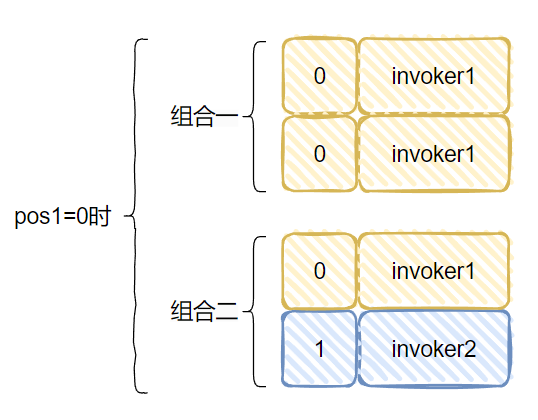
针对组合一,又因为有这个判断在这里:
if (pos2 == pos1) {
pos2 = pos2 + 1;
}当 pos2 = pos1,即随机到同一个下标的时候,pos2 需要加一,以免使用同一个 invoker。
所以,当 pos1=0 时,随机的最终只会是这两种情况:

pos1=1
同理,我们可以得出 pos1=1 时,情况是这样的:
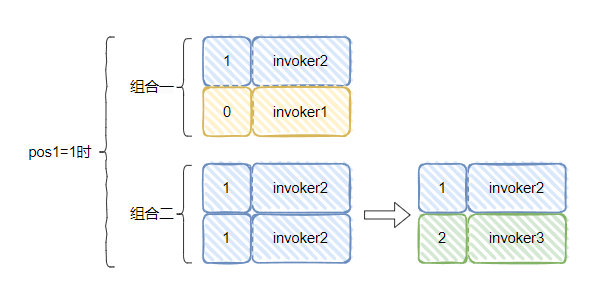
pos1=2
当 pos1=2 时,情况是这样的:
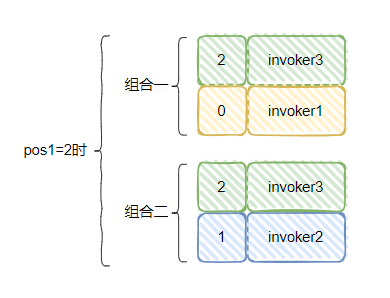
汇总
此时,我们所有情况都分析完成了,穷举大法已经使用完毕。
这个时候我们把所有的情况组合起来看一下:
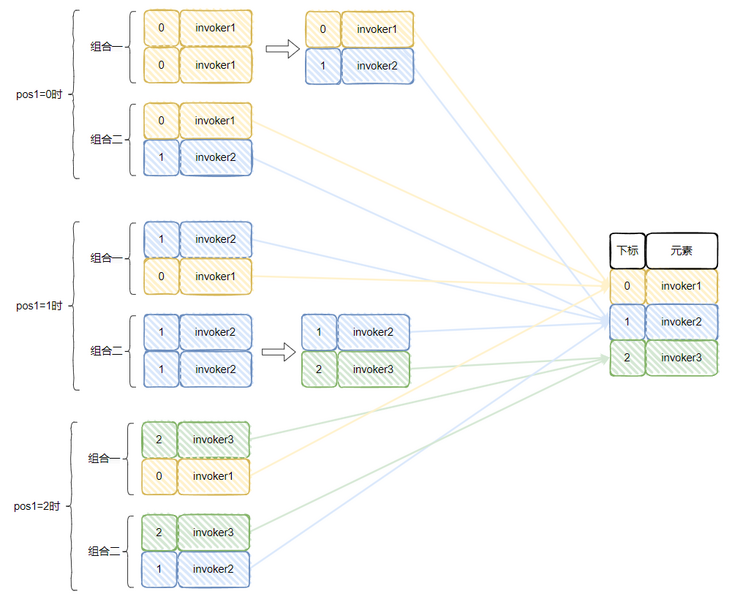
- invoker1 被选中了 4 次
- invoker2 被选中了 5 次
- invoker3 被选中了 3 次
来,请你大声点的告诉我,这个算法是不是公平的?

都不是 1:1:1 了,还公平个啥啊。
所以,我在之前的文章里面是这样说的:

事实也证明了,确实是对于最后一个元素是不公平的。
于是,我开始准备着手敲代码,打算再混一个 pr。
我想换成的源码也很简单。因为它核心目标是从 list 集合中随机返回两个对象嘛。
那我直接就是这样:
Object invoker1 = invokerList.remove(ThreadLocalRandom.current().nextInt(invokerList.size()));
Object invoker2 = invokerList.remove(ThreadLocalRandom.current().nextInt(invokerList.size()));你仔细的嗦一嗦这个代码,是不是很公平?
当一个元素被选中之后,我就把它给踢出去。这样第二次随机的时候,invokerList.size() 的值就实现了减一的逻辑。
既可以保证第二次随机的时候,不会随机到一样的元素。
也可以保证剩下的每个元素都有机会再次参与到随机过程中。

为此,我还专门写了一个 Demo 来验证这个写法:
public class MainTest {
private final static HashMap COUNT_MAP = new HashMap();
public static void main(String[] args) {
for (int i = 0; i list = new ArrayList();
list.add(1);
list.add(2);
list.add(3);
Integer invoker1 = list.remove(ThreadLocalRandom.current().nextInt(list.size()));
Integer invoker2 = list.remove(ThreadLocalRandom.current().nextInt(list.size()));
posCount(invoker1);
posCount(invoker2);
}
System.out.println(COUNT_MAP);
}
public static void posCount(Integer key) {
Integer pos1Integer = COUNT_MAP.get(key);
if (pos1Integer == null) {
COUNT_MAP.put(key, 1);
} else {
pos1Integer++;
COUNT_MAP.put(key, pos1Integer);
}
}
}你粘过去就能跑,运行 10w 次,每个元素被选中的总次数基本上就是 1:1:1。
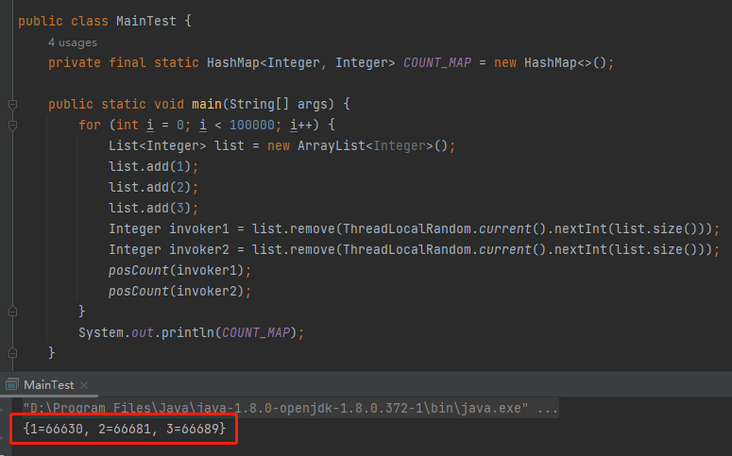
而把 Dubbo 源码里面的实现拿过来:
public class MainTest {
private final static HashMap COUNT_MAP = new HashMap();
public static void main(String[] args) {
List list = new ArrayList();
list.add(1);
list.add(2);
list.add(3);
int length = list.size();
for (int i = 0; i = pos1) {
pos2 = pos2 + 1;
}
posCount(pos1);
posCount(pos2);
}
System.out.println(COUNT_MAP);
}
public static void posCount(Integer key) {
Integer pos1Integer = COUNT_MAP.get(key);
if (pos1Integer == null) {
COUNT_MAP.put(key, 1);
} else {
pos1Integer++;
COUNT_MAP.put(key, pos1Integer);
}
}
}也跑 10w 次,运行结果是这样的:
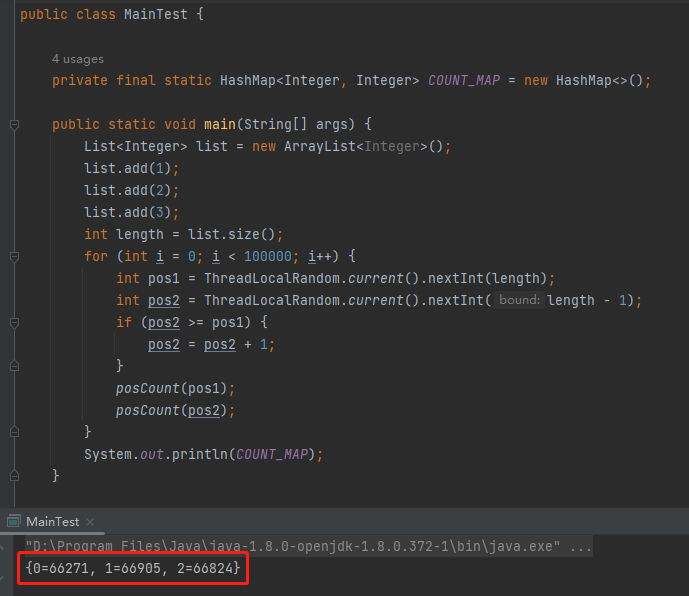
…
…
…
卧槽,等等,怎么回事,居然也是接近 1:1:1 的?
我当时看到这个运行结果的时候,表情大概是这样的:

这玩意,和我分析出来的不一样啊。
反转
其实也不能算是反转吧。
因为我前面分析的时候,给的代码是这样的:
if (pos2 == pos1) {
pos2 = pos2 + 1;
}而真实的源码是这样的:
if (pos2 >= pos1) {
pos2 = pos2 + 1;
}一个是 ==,一个 >=。
当我把这里换成 == 的时候,运行结果就不再是 1:1:1 了,符合我前面穷举大法分析的情况。

而在我的潜意识里面,第一次看代码的时候,我一直以为这个部分的代码就是 ==,所以我一直按照 == 进行的分析,从而觉得它有问题。
这波,我觉得得让潜意识来背锅。

当是 >= 的时候,我们只需要重新分析一下 pos1=0 的情况。
组合一,0>=0,满足条件,最终 pos1=0,pos2 会加一,变成 1,所以还是会变成之前分析的情况:
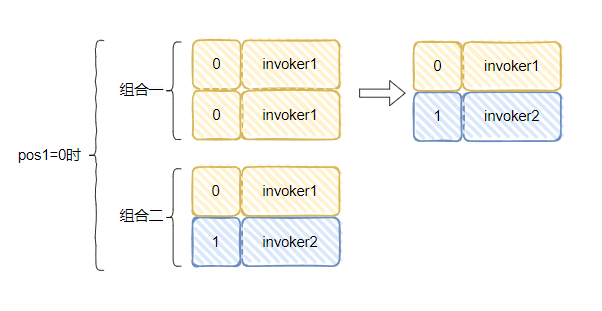
当时对于组合二,情况就发生了微妙的变化。
组合二,1>=0,满足条件,最终 pos1=0,pos2 会加一,变成 2,所以就变成了这样:
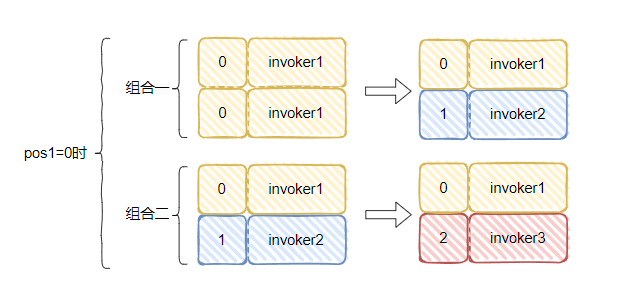
invker2 被替换为了 invoker3。
还记得我们之前,按照 == 的情况,分析出来的比例吗?
- invoker1 被选中了 4 次
- invoker2 被选中了 5 次
- invoker3 被选中了 3 次
此时,我们按照 >= 的情况分析,invoker2 被替换为了 invoker3。
那么比例就变成了:
- invoker1 被选中了 4 次
- invoker2 被选中了 4 次
- invoker3 被选中了 4 次
所以,回到我最最开始说的读者提出的第二个问题:
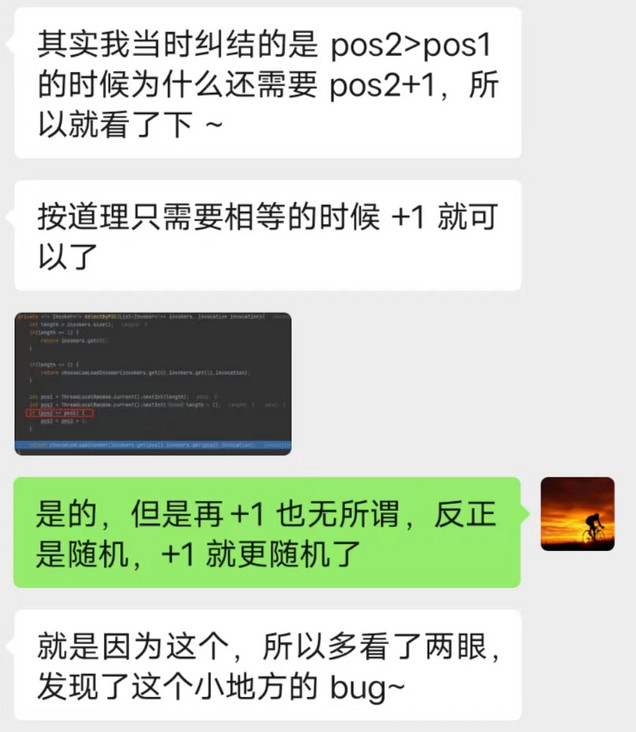
我在回答读者的时候,也是认为 == 就行了,虽然不公平,但是也不是不能用。
但是经过前面这一波分析。
为什么一定要是 >=,而不能只是 == 呢?
之前,我一直认为不公平是因为我认为最后一个元素少参与了一次随机。
但是,由于 >= 的存在,并不会存在这种情况。
啊,为什么会产生一种让我想要跪下的感觉?
数学,是因为我在里面加了数学。
神奇的、令人又上头又着迷的数学。
荒腔走板
在这个事情上,我整个心态是从自信满满到一地鸡毛,这个心路历程让我想起了我大学的时候,学过的一门课程叫做《线性代数》。
当时我学的可认真,老师讲的每节课我感觉我都听懂了,期末考试的过程中,包括考完之后我都是信心满满的样子,觉得这题也不难啊。
随随便便考个八十多分问题不大吧。
最后,考试结果出来的时候我没及格,我记得是 56 分还是 58 分的样子,反正差一点点及格,这课居然挂了?
我当时在宿舍就拍案而起:肯定有问题,我要求查卷,我做题的时候很有自信啊。
然后我要到了老师的联系方式,并自报家门,说明情况,我坚持认为应该是某个环节出了问题,看看能不能把卷子找出来再看看。
后来啊…
老师把卷子拍照发给我了,确实是某个环节出了问题,这个环节就是我自己。
我和答案对了一下,卷面就只有 40 多分的样子。
最终成绩有 50 多分是因为老师还算了平时分,由上课出勤率和日常作业完成情况综合算出来的。
那天,我站在宿舍的阳台上,看着手机上的试卷照片,再挑眼看向远方,夕阳西下,残阳如血,六楼的风儿甚至喧嚣,肆意的在我脸上拂过。
楼下熙熙攘攘的学生走过,时不时的爆发出一阵阵银铃般的笑声,我只是觉得吵闹。
随后,我问室友:什么时候补考?有没有人能给我补习一下?
数学,啊,这神奇的、令人又上头又着迷的数学。


