1775. 通过最少操作次数使数组的和相等(难度:中等)
一、题目
给你两个长度可能不等的整数数组 nums1 和 nums2 。两个数组中的所有值都在 1 到 6 之间(包含 1 和 6)。
每次操作中,你可以选择 任意 数组中的任意一个整数,将它变成 1 到 6 之间 任意 的值(包含 1 和 6)。
请你返回使 nums1 中所有数的和与 nums2 中所有数的和相等的最少操作次数。如果无法使两个数组的和相等,请返回 -1。
二、示例
2.1> 示例 1:
【输入】nums1 = [1,2,3,4,5,6], nums2 = [1,1,2,2,2,2]
【输出】3
【解释】你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums2[0] 变为 6 。 nums1 = [1,2,3,4,5,6], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[5] 变为 1 。 nums1 = [1,2,3,4,5,1], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[2] 变为 2 。 nums1 = [1,2,2,4,5,1], nums2 = [6,1,2,2,2,2] 。
2.2> 示例 2:
【输入】nums1 = [1,1,1,1,1,1,1], nums2 = [6]
【输出】-1
【解释】没有办法减少 nums1 的和或者增加 nums2 的和使二者相等。
2.3> 示例 3:
【输入】nums1 = [6,6], nums2 = [1]
【输出】3
【解释】你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums1[0] 变为 2 。 nums1 = [2,6], nums2 = [1] 。
- 将 nums1[1] 变为 2 。 nums1 = [2,2], nums2 = [1] 。
- 将 nums2[0] 变为 4 。 nums1 = [2,2], nums2 = [4] 。
提示:
-
110^5 -
16
三、解题思路
首先,根据题意,我们需要计算出数组nums1和nums2之间,最小的操作次数,使得nums1的总和:sum(nums1)与nums2的总和:sum(nums2)两个值相等。那么我们可以根据如下4个步骤来解决这个问题:
【步骤1】分别计算sum(nums1)和sum(nums2)的值,确定两个数组加和的差值diff,以及sum(nums1)和sum(nums2)之间的大小关系。
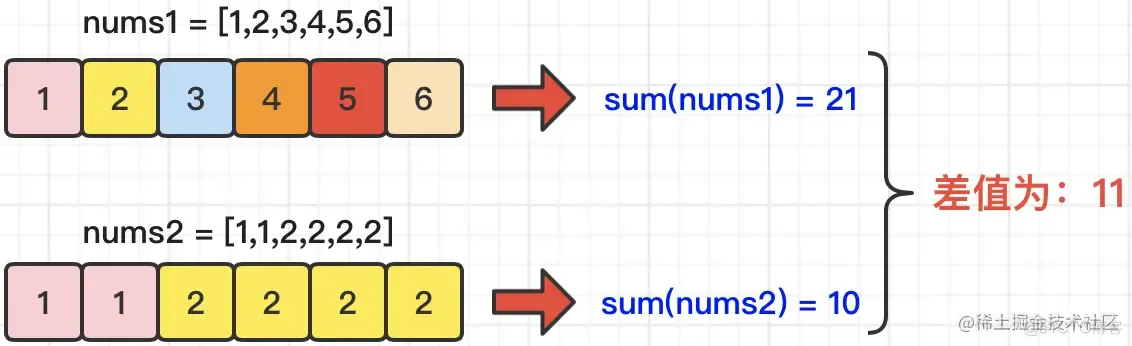
【步骤2】将总和较小的数组赋值为int[] smaller,将总和较大的数组赋值为int[] bigger。
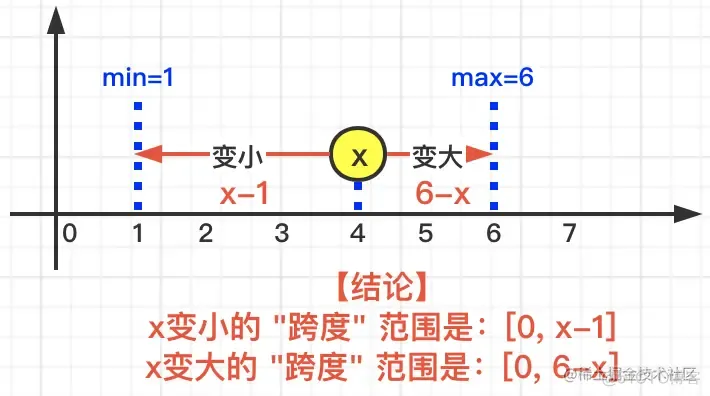
对于
smaller数组中的每个值,我们要执行变大操作,其中:由于最大值是6,所以每个元素s变大的最大跨度是:6 - s;
对于bigger数组中的每个值,我们要执行变小操作,其中:由于最小值是1,所以每个元素b变大的最大跨度是:b - 1;
【步骤3】创建一个用于存储跨度&出现次数的数组int[] range(也可以采用Map结构),其中:下标index表示跨度值,range[index]表示该跨度值出现的次数。由于题目中指出,nums1和nums2中元素的值的范围是[1, 6],所以,对应的跨度值就是[0, 5]。为了便于画图,图中采用Map结构表示:
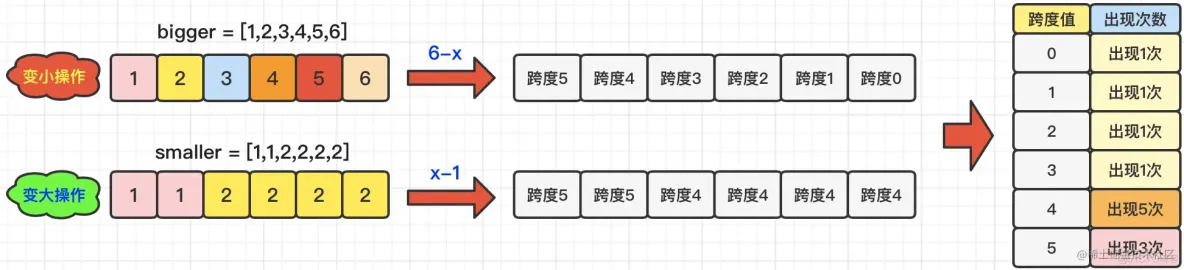
【步骤4】由于要求计算出最小操作次数,所以我们需要从range数组末尾开始遍历执行对比操作,以上面图中的例子做演示,diff=11,range=[1,1,1,1,5,3]:
【第1次操作】因为差值diff > 跨度5,所以差值diff变为
6(11减5),range[5]的出现次数变为2(3减1);
【第2次操作】因为差值diff > 跨度5,所以差值diff变为1(6减5),range[5]的出现次数变为1(2减1);
【第3次操作】因为差值diff ,满足题解,返回最少操作次数为:3。
四、代码实现
class Solution {
public int minOperations(int[] nums1, int[] nums2) {
int result = 0, l1 = nums1.length, l2 = nums2.length, sum1 = 0, sum2 = 0, diff;
if (6 * l1 = 0; i--) { // 从最大的差值开始对比
while (range[i] > 0) { // 如果差值range[i]出现的次数不为0
result++; // 操作次数加1
if (i >= diff) return result; // 如果差值大于等于diff,则操作结束,返回操作数result
range[i]--; // 差值range[i]的出现次数减1
diff -= i; // 更新diff值
}
}
return -1;
}
// 计算每个差值(1~5)出现的次数
private int[] calculate(int[] nums1, int[] nums2, int sum1, int sum2) {
int[] bigger = (sum1 
图解LeetCode——1812. 判断国际象棋棋盘中一个格子的颜色(难度:简单)
一、题目
给你一个坐标 coordinates ,它是一个字符串,表示国际象棋棋盘中一个格子的坐标。下图是国际象棋棋盘示意图。

如果所给格子的颜色是白色,请你返回 true,如果是黑色,请返回 false 。
给定坐标一定代表国际象棋棋盘上一个存在的格子。坐标第一个字符是字母,第二个字符是数字。
二、示例
2.1> 示例 1:
【输入】coordinates = “a1”
【输出】false
【解释】如上图棋盘所示,”a1″ 坐标的格子是黑色的,所以返回 false 。
2.2> 示例 2:
【输入】coordinates = “h3”
【输出】true
【解释】如上图棋盘所示,”h3″ 坐标的格子是白色的,所以返回 true 。
2.3> 示例 3:
【输入】coordinates = “c7”
【输出】false
提示:
- coordinates.length ==
2 - ‘
a‘ h’ - ‘
1‘ 8’
三、解题思路
3.1> 采用异或方式
首先:针对题目中的棋盘,我们可以针对 行 和 列 ,做出如下假设性的拆分操作:
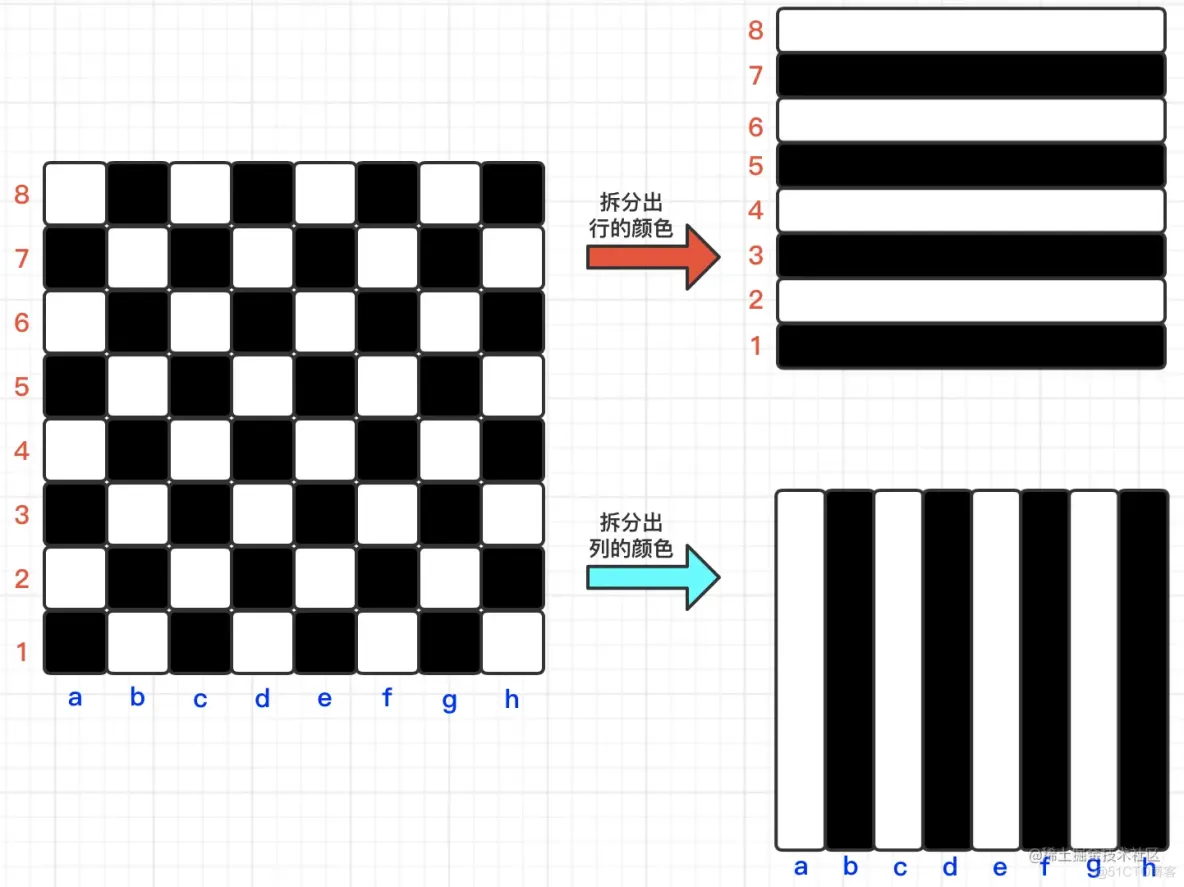
【棋盘中列的假设】:
a列白色、b列黑色、c列白色、d列黑色……
【棋盘中行的假设】:1行黑色、2行白色、3行黑色、4行白色……
然后,我们再观察棋盘中的格子,发现如下规律:
【规律1:白色 + 黑色 = 黑色】
以a1为例,此格子是黑色的,由于这个格子是由a列+1行组成,即:a列(白色) + 1行(黑色) = a1(黑色);
【规律2:白色 + 白色 = 白色】
以a2为例,此格子是白色的,由于这个格子是由a列+2行组成,即:a列(白色) + 2行(白色) = a2(白色);
【规律3:黑色 + 黑色 = 白色】
以b1为例,此格子是白色的,由于这个格子是由b列+1行组成,即:b列(黑色) + 1行(黑色) = b1(白色);
最后,我们发现这种规律与 异或操作 是一样的,即:白色用0表示,黑色用1表示:
【规律1:白色 + 黑色 = 黑色】0^1等于1
【规律2:白色 + 白色 = 白色】0^0等于0
【规律3:黑色 + 黑色 = 白色】1^1等于0
所以,我们只需要将coordinates指定的行和列转换为0或1,然后计算异或即可。
3.2> 采用奇偶方式
我们以a1格子为例,a的ASCII码为97,1的ASCII码为49,那么ASCII(a) + ASCII(1) = 97 + 49 = 146,那么当总和是偶数时,则格子是黑色;如果总和是奇数时,则格子是白色。
此处就不再画图赘述了。
四、代码实现
4.1> 采用异或方式
class Solution {
public boolean squareIsWhite(String coordinates) { // 白色用0表示,黑色用1表示
int letter = (coordinates.charAt(0) - 'a') % 2; // a列:白色 b列:黑色 c列:白色 ……
int number = (coordinates.charAt(1) - '1' + 1) % 2; // 1行:黑色 2行:白色 3行:黑色 ……
return (letter ^ number) == 0;
}
}
4.2> 采用奇偶方式
class Solution {
public boolean squareIsWhite(String coordinates) {
return (coordinates.charAt(0) + coordinates.charAt(1)) % 2 == 1; // 白色用奇数表示,黑色用偶数表示
}
}
1780. 判断一个数字是否可以表示成三的幂的和(难度:中等)
一、题目
给你一个整数 n ,如果你可以将 n 表示成若干个不同的三的幂之和,请你返回 true ,否则请返回 false 。
对于一个整数 y ,如果存在整数 x 满足 y == 3^x ,我们称这个整数 y 是三的幂。
二、示例
2.1> 示例 1:
【输入】n = 12
【输出】true
【解释】12 = 3^1 + 3^2
2.2> 示例 2:
【输入】n = 91
【输出】true
【解释】91 = 3^0 + 3^2 + 3^4
2.3> 示例 3:
【输入】n = 21
【输出】false
提示:
-
110^7
三、解题思路
根据题目表述,我们要判断n是否满足三的幂之和,其实关于这道题,如果我们将三的幂之和改变为二的幂之和,就清晰多了。因为我们常用的二进制转成十进制,就是采用二的幂之和来计算获得了。那么,同理,我们采用三进制计算的方式,就可以获得这道题的答案了。
也就是说,我们通过对n进行除3取余操作,如果获得0或1,则表示满足三进制,依次类推,直到除完为止。如果在除3取余过程中,不满足0或者1,则直接返回false。具体逻辑,请参照下图所示:
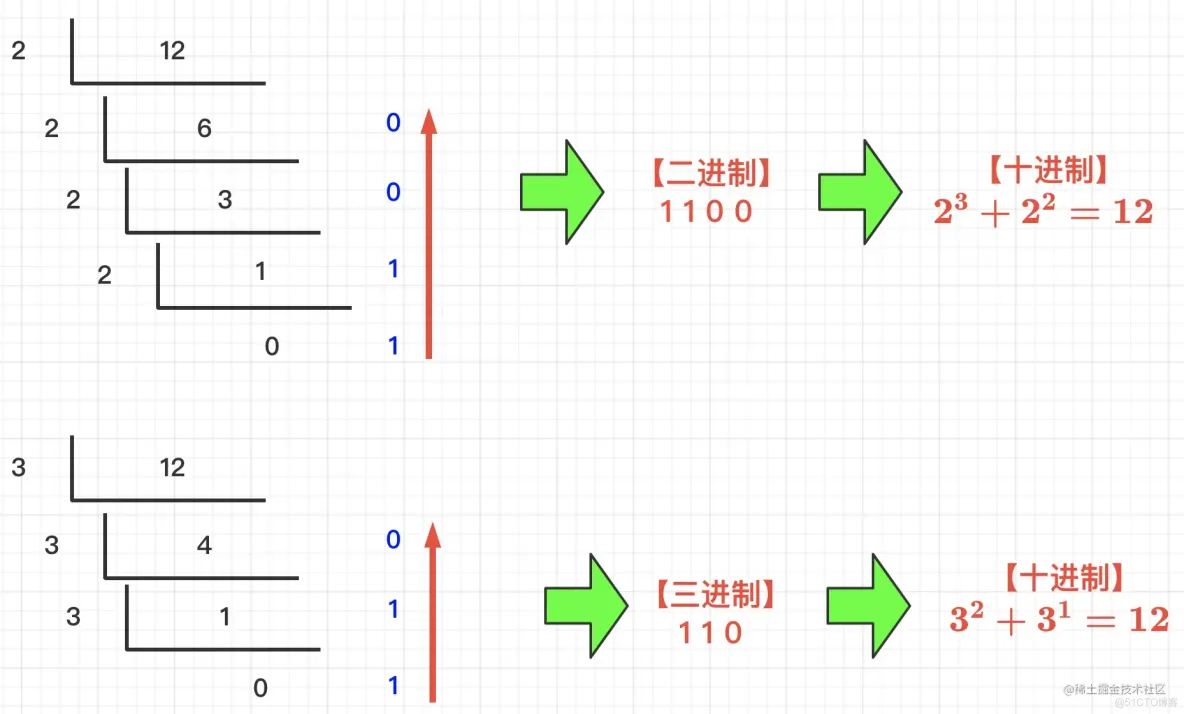
四、代码实现
class Solution {
public boolean checkPowersOfThree(int n) {
while (n != 0) {
if (n % 3 == 0 || n % 3 == 1) n = n / 3; // 满足三进制
else return false; // 不满足三进制,返回false
}
return true;
}
}
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ (^o^)/ ~ 「干货分享,每天更新」


