2022.8.7更新
学习js的过程中发现了0.1+0.2更深一层的运算过程,感兴趣的可以看看这个博主写的帖子。
JavaScript 浮点数之迷:0.1 + 0.2 为什么不等于 0.3?
前提:
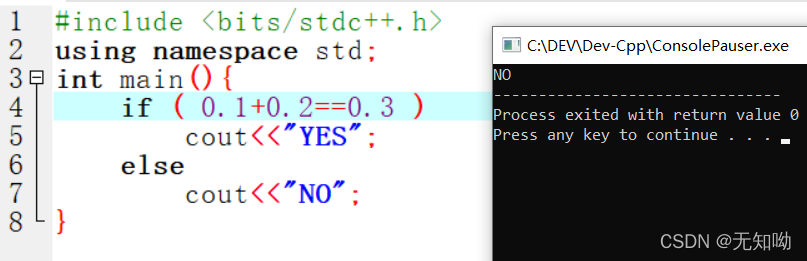
由于存在精度限制,浮点数只是⼀个近似值,它的计算是不精确的,⽐如
C
语⾔⾥⾯
0.1 + 0.2
并
C
语⾔⾥⾯
0.1 + 0.2
并
不等于
0.3
,⽽是有⼀个很⼩的误差。
0.3
,⽽是有⼀个很⼩的误差。
if
(
0.1
+
0.2
==
0.3
)
// false
(
0.1
+
0.2
==
0.3
)
// false
PS:正确的判断两数是否相等的条件是看两数的
绝对值之差是否小于1e-5
绝对值之差是否小于1e-5

C
语⾔允许使⽤科学计数法表示浮点数,使⽤字⺟
e
来分隔⼩数部分和指数部分。
语⾔允许使⽤科学计数法表示浮点数,使⽤字⺟
e
来分隔⼩数部分和指数部分。
上⾯示例中,
e
后⾯如果是加号
+
,加号可以省略。注意,科学计数法⾥⾯
e
的前后,不能存在空格。
e
后⾯如果是加号
+
,加号可以省略。注意,科学计数法⾥⾯
e
的前后,不能存在空格。
double
x
=
123.456e+3
;
// 123.456 x 10^3
x
=
123.456e+3
;
// 123.456 x 10^3
//
等同于
等同于
double
x
=
123.456e3
;
x
=
123.456e3
;
另外,科学计数法的⼩数部分如果是
0.x
或
x.0
的形式,那么
0
可以省略。
0.x
或
x.0
的形式,那么
0
可以省略。
0.3E6
//
等同于
等同于
.
3E6
3E6
3.0E6
//
等同于
等同于
3.E6
总结 合法浮点数的三种形式:
1. 十进制小数形式。由数字和小数点组成,必须有小数点。例如(123.)(123.0)(.123)。
2. 指数形式。如123e3。字母e(或E)之前必须有数字,e后面的指数必须为整数。
3. 规范化的指数形式里面,小数点前面有且只有一位非零的数字。如1.2345e8


