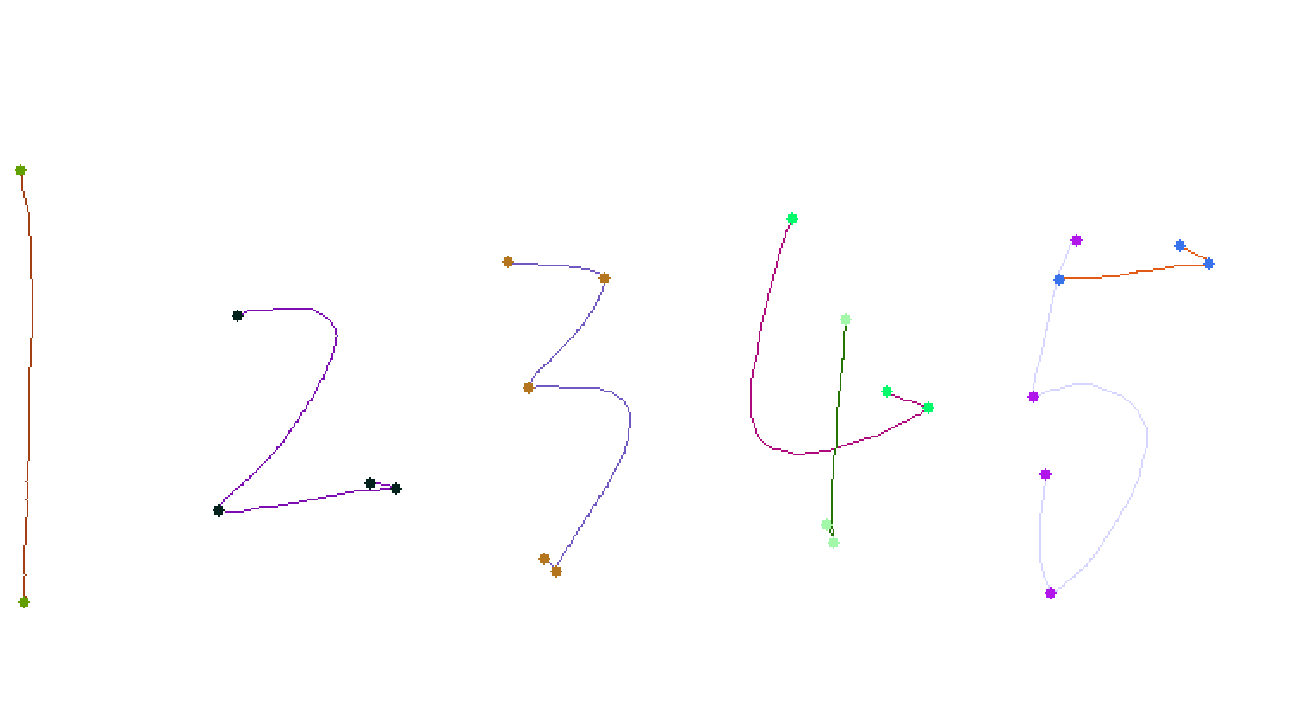文章目录
-
- 一、线段曲率计算原理
- 二、线段拐点提取流程
- 三、python实现拐点的提取
-
- 3.1、曲线的点的平滑
-
- 3.1.1、一次贝塞尔曲线拟合
- 3.1.2、二次贝塞尔曲线拟合
- 3.2、拐点的计算
-
- 3.2.1、Bending value的计算
- 3.2.2、判断三点是否在同一条直线上
- 3.2.3、计算拐点
一、线段曲率计算原理
一般的曲率计算方法,如玄长比例法、三次B样条表达、线性多边形逼近和局部对称等方法。今天主要介绍 弯曲值算法(Bending value) 算法。其表达式为:
b
i
k
=
m
a
x
(
∣
(
x
i
−
k
−
x
i
)
+
(
x
i
+
k
−
x
i
)
)
∣
,
∣
(
y
i
−
k
−
y
i
)
+
(
y
i
+
k
−
y
i
)
∣
)
b_{ik}=max(|(x_{i-k}-x_{i})+(x_{i+k}-x_{i}))|,|(y_{i-k}-y_{i})+(y_{i+k}-y_{i})|)
bik=max(∣(xi−k−xi)+(xi+k−xi))∣,∣(yi−k−yi)+(yi+k−yi)∣)
计算Bending Value的示意图如下:
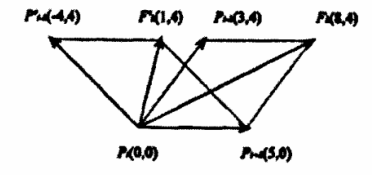

参考链接:
手写体汉字的书写质量评价
二、线段拐点提取流程
-
计算线段上每一点的Bending Value,记作
B
v
(
i
)
Bv(i)
Bv(i),这里需要初始化阈值
delta=1.1和搜索范围k=1 -
当
B
v
(
i
)
>
d
e
l
t
a
Bv(i)>delta
Bv(i)>delta,且对于所有
i
−
k
i−k=j=i+k,均有
B
v
(
i
)
>
=
B
v
(
j
)
Bv(i)>=Bv(j)
Bv(i)>=Bv(j),则该点符合局部曲率最大的性质,作为候选拐点。
-
筛选条件一:判断候选拐点相邻三点
p
i
−
1
p_{i-1}
pi−1、
p
i
p_{i}
pi、
p
i
+
1
p_{i+1}
pi+1是否位于同一条直线上,如果在则排除该点
-
筛选条件二:计算自适应弯曲值(Bending Value)。算法流程如下:
计算候选点的搜索范围k从1开始增加,用
b
i
k
b_{ik}
bik表示当前Bending Value。如果
b
i
k
>
=
b
i
k
+
1
b_{ik}>=b_{ik+1}
bik>=bik+1,k增加1,否则停止增加。求得连续的Bending Value值后,需要再进行求平均值,作为最终该点的弯曲值,计算公式如下:
b
v
i
=
1
k
i
∑
j
=
1
k
i
b
i
j
b_{v_{i}}=frac{1}{k_{i}}sum^{k_{i}}_{j=1}b_{ij}
bvi=ki1j=1∑kibij
根据计算的自适应拐点,还需要满足以下条件:- 条件一:
b
v
i
bvitheta
- 条件二:
b
v
i
bvibvj
,对于j
=
i
−
1
j=i-1
j=i−1或j
=
i
+
1
j=i+1
j=i+1
- 条件三:
b
v
i
=
b
v
i
−
1
b_{v_{i}}=b_{v_{i-1}}
bvi=bvi−1,并且k
i
kiki−1
- 条件四:
b
v
i
=
b
v
i
+
1
b_{v_{i}}=b_{v_{i+1}}
bvi=bvi+1,并且k
i
ki=ki+1
条件一表示Bending Value值应大于阈值,条件二、三、四表示拐点必须为局部最大值
- 条件一:
三、python实现拐点的提取
3.1、曲线的点的平滑
当获取曲线的点整后点与点之间可能存在较大的间隔,需要我们对这些点进行一个采样来增加其连续性。一般采样方法有DDA、一次贝塞尔曲线拟合、二次贝塞尔曲线拟合或三次贝塞尔曲线离合。其中DDA和一次贝塞尔曲线拟合类似。都是通过两点之间直线的斜率来进行一个采样,当然使用更高阶的方法,采样曲线也更加平滑。
3.1.1、一次贝塞尔曲线拟合
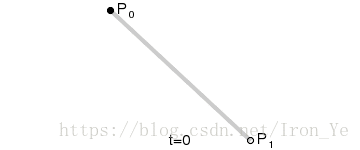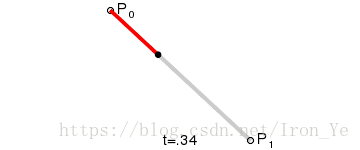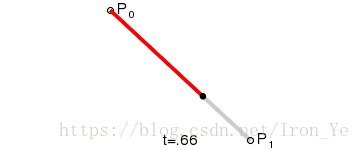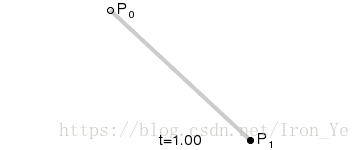
如上图所示,对于平面上的两个点 P0 和 P1,假设另一点 B 匀速地从 P0 点运动到 P1 点,则有 B 点在 t 时刻的坐标公式:
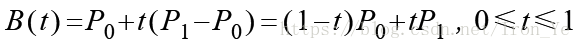
将 B 点在各个时刻的坐标依次连接起来所形成的线,就是所谓的贝塞尔曲线。此公式表示的是一次贝塞尔曲线,也称为线性贝塞尔曲线。
python实现如下:
def getFirstBezierPointByT(start,end,t):
'''
根据一次贝尔曲线的的计算公式计算各个时刻的坐标值
:param start:
:param end:
:param t:
:return:
'''
x=(1-t)*start[0]+t*end[0]
y=(1-t)*start[1]+t*end[1]
return [x,y]
def calculateFirstBezierPoints(start,end):
'''
计算两点之间的塞尔曲线点集
:param start:
:param handle:
:param end:
:return:
'''
bx=start[0]
by=start[1]
ex=end[0]
ey=end[1]
beDis=math.sqrt(math.pow((bx-ex),2)+math.pow((by-ey),2))
count=int(beDis//1)
if count2:
return [start]
step = 1.0 / count
points=[]
t = 0.0
for i in range(count):
points.append(getFirstBezierPointByT(start, end, t))
t += step
return points
def firstBezierCurveFitting(pts):
'''
一次贝塞尔曲线拟合
:param pts:
:return:
'''
new_pts = []
for pt in pts:
new_pt = []
for i in range(0, (len(pt) - 1)):
pp=calculateFirstBezierPoints(pt[i], pt[i + 1])
new_pt += pp
new_pt.append(pt[len(pt)-1])
new_pts.append(new_pt)
return new_pts
3.1.2、二次贝塞尔曲线拟合
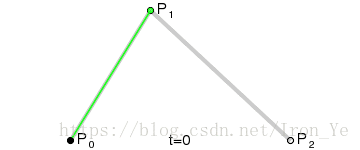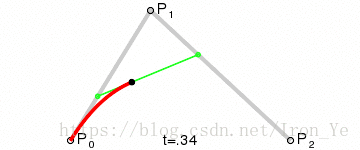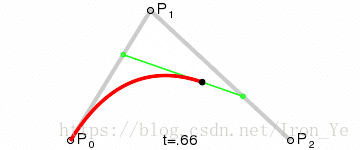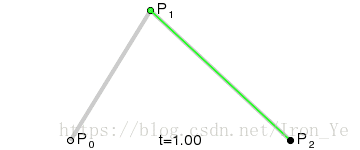
同样地,对于平面上的三个点 P0、P1 和 P2 ,假设 P0P1 之间有个点 B1 匀速地从 P0 运动到 P1 ,P1P2 之间有个点 B2 匀速地从 P1 运动到 P2,则有:
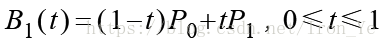
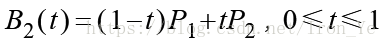
假设另一点 B 匀速地从 B1 运动到 B2,则有 B 点的坐标公式:

将 B1 和 B2 的坐标公式代入上面的表达式,整理后得到 B 点的坐标公式:

B 点在各个时刻的坐标所连成的曲线即为二次贝塞尔曲线,其中 P0 和 P2 称为 数据点,P1 称为 控制点 。
具体python实现可以参考如下链接实现。
参考链接:
一种简单的贝塞尔拟合算法
3.2、拐点的计算
3.2.1、Bending value的计算
def computeBendingValue(p1,p2,p3):
'''
计算弯曲值
:param p1:
:param p2:
:param p3:
:return:
'''
return max(abs(p1[0]+p3[0]-2*p2[0]),abs(p1[1]+p3[1]-2*p2[1]))
3.2.2、判断三点是否在同一条直线上
def isSameGradient(p1,p2,p3):
'''
判断相邻三点是否在同一条直线上
:param p1:
:param p2:
:param p3:
:return:
'''
g1=(p1[1]-p2[1])/(p1[0]-p2[0]+0.00001)
g2=(p2[1]-p3[1])/(p2[0]-p3[0]+0.00001)
return g1==g2
3.2.3、计算拐点
计算拐点时,需要有些核心注意点:
-
计算笔迹端点的Bending value,需要进行一些预处理,我的处理如下:
#当位于左端点的时候 if i-k0: p1=pt[i] else: p1=pt[i-k] #当位于右端点的时候 if i+k>=len(pt): p3=pt[i] else: p3=pt[i+k] -
如何计算自适应Bending value
k0=1 bv0=0 bv_list=[] # 计算候选拐点所有的Bending Value曲率,直到最大值为止 while k0+ilen(pt) and i-k0>0: bv0=computeBendingValue(pt[i-k0],pt[i],pt[i+k0]) if bv0>=bv: bv_list.append(bv0) bv=bv0 k0+=1 if bv0bv: break k_list[i]=k0 # 计算所有曲率的平均值,作为最终的候选点的曲率 if len(bv_list)==0: avg_bv=bv else: avg_bv=sum(bv_list)/len(bv_list) -
进一步筛选拐点的实现
# 条件一:bv# 条件二:bvi # 条件三:bvi==bvi-1 and ki # 条件四:bvi==bvi+1 and ki # 条件一表示Bending Value应该大于theta;条件二~四表示Bending Value应该为局部最大值 if avg_bv1.1 or (curvs[i] curvs[i - 1] or curvs[i] curvs[i + 1]) or (curvs[i]==curvs[i-1] and k_list[i]k_list[i-1]) or (curvs[i]==curvs[i+1] and k_list[i]k_list[i+1]): continue else: result.append(i) -
最后还需要进一步合并相邻的拐点
merge_result=[] i=0 tmp=[] while i+1len(result_1): if result_1[i+1]-result_1[i]5: tmp.append(result_1[i]) if i+1==len(result_1)-1: tmp.append(result_1[i+1]) merge_result.append(tmp) tmp=[] else: tmp.append(result_1[i]) merge_result.append(tmp) tmp=[] if i + 1 == len(result_1) - 1: merge_result.append([result_1[i+1]]) i=i+1 # 合并最终的结果 new_result=[] for res in merge_result: avg_res=sum(res)//len(res) new_result.append(avg_res)
因为项目原因,不方便提供完整代码,但核心点已经给出,方便大家参考。最终结果如下: